Analyzing Features¶
Rates¶
In [1]:
import impact as impt
# import cobra
# import cobra.test
# import cobra.io
import numpy as np
# import matplotlib.pyplot as plt
% matplotlib inline
from plotly.offline import download_plotlyjs, init_notebook_mode, plot, iplot
from plotly.graph_objs import Bar, Layout, Figure, Scatter
init_notebook_mode()
# We include this to ensure the js is loaded when viewed online
from IPython.display import HTML
HTML('<script src="https://cdn.plot.ly/plotly-latest.min.js"></script>')
C:\Users\Naveen\Anaconda3\lib\site-packages\IPython\html.py:14: ShimWarning: The `IPython.html` package has been deprecated. You should import from `notebook` instead. `IPython.html.widgets` has moved to `ipywidgets`.
"`IPython.html.widgets` has moved to `ipywidgets`.", ShimWarning)
C:\Users\Naveen\Anaconda3\lib\site-packages\sqlalchemy\orm\mapper.py:1703: SAWarning: Implicitly combining column experiment.id with column stage.id under attribute 'id'. Please configure one or more attributes for these same-named columns explicitly.
util.warn(msg)
In [2]:
# Let's grab the iJO1366 E. coli model, cobra's test module has a copy
model = cobra.test.create_test_model("ecoli")
# Simulate anaerobic conditions by prevent oxygen uptake
model.reactions.get_by_id('EX_o2_e').knock_out()
# Optimize the model
cobra.flux_analysis.optimize_minimal_flux(model)
model.summary()
# Let's consider one substrate and five products
biomass_keys = ['Ec_biomass_iJO1366_core_53p95M']
substrate_keys = ['EX_glc_e']
product_keys = ['EX_for_e','EX_ac_e','EX_etoh_e','EX_succ_e']
analyte_keys = biomass_keys+substrate_keys+product_keys
# We'll use numpy to generate an arbitrary time vector
# The initial conditions (mM) [biomass, substrate,
# product1, product2, ..., product_n]
y0 = [0.05, 100, 0, 0, 0, 0]
t = np.linspace(0,16,8)
# Returns a dictionary of the profiles
from impact.helpers.synthetic_data import generate_data
dFBA_profiles = generate_data(y0, t, model,
biomass_keys, substrate_keys,
product_keys, plot = True)
IN FLUXES OUT FLUXES OBJECTIVES
glc__D_e -10.00 h_e 27.87 Ec_biomass_iJO1366_core_53p95M 0.242
nh4_e -2.61 for_e 17.28
h2o_e -1.71 ac_e 8.21
pi_e -0.23 etoh_e 8.08
co2_e -0.09 succ_e 0.08
so4_e -0.06 5drib_c 0.00
k_e -0.05 glyclt_e 0.00
mg2_e -0.00 mththf_c 0.00
fe2_e -0.00 4crsol_c 0.00
fe3_e -0.00 meoh_e 0.00
ca2_e -0.00 amob_c 0.00
cl_e -0.00
cu2_e -0.00
mn2_e -0.00
zn2_e -0.00
ni2_e -0.00
mobd_e -0.00
cobalt2_e -0.00
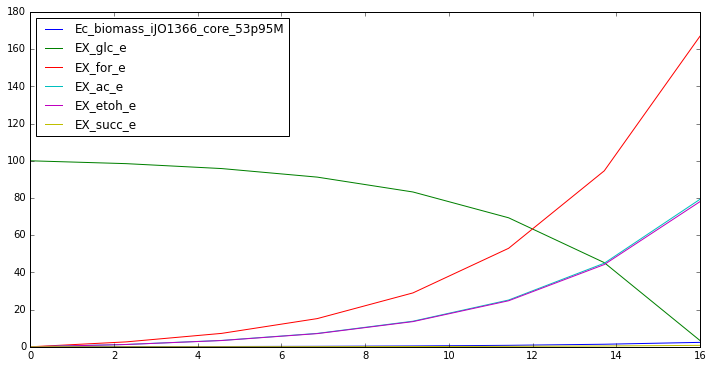
Now that we have a simulated ‘two-stage’ fermentation data, let’s try to analyze it. First let’s try to curve fit and pull parameters from the overall data
In [3]:
# These time courses together form a single trial
single_trial = impact.SingleTrial()
for analyte in analyte_keys:
# Instantiate the timecourse
timecourse = impact.TimeCourse()
# Define the trial identifier for the experiment
# timecourse.trial_identifier.analyte_name = analyte
timecourse.trial_identifier = impt.TrialIdentifier(strain=impt.Strain(nickname='teststrain'), analyte_name = analyte)
if analyte in biomass_keys:
timecourse.trial_identifier.analyte_type = 'biomass'
elif analyte in substrate_keys:
timecourse.trial_identifier.analyte_type = 'substrate'
elif analyte in product_keys:
timecourse.trial_identifier.analyte_type = 'product'
else:
raise Exception('unid analyte')
timecourse.time_vector = t
timecourse.data_vector = dFBA_profiles[analyte]
single_trial.add_analyte_data(timecourse)
single_trial.calculate()
# # Add this to a replicate trial (even though there's one replicate)
# replicate_trial = impact.ReplicateTrial()
# replicate_trial.add_replicate(single_trial)
# # Add this to the experiment
# experiment = impact.Experiment(info = {'experiment_title' : 'test experiment'})
# experiment.add_replicate_trial(replicate_trial)
# import plotly.offline
# plotly.offline.init_notebook_mode()
# fileName = impact.printGenericTimeCourse_plotly(replicateTrialList=[replicate_trial],
# titersToPlot=biomass_keys, output_type='image',)
# from IPython.display import Image
# Image(fileName)
In [4]:
# We can query the rates instead.
for keys in [biomass_keys,substrate_keys,product_keys]:
# plt.figure()
data = []
for analyte in keys:
trace = Scatter(x=t,
y=single_trial.analyte_dict[analyte].gradient,
name = analyte)
data.append(trace)
fig = Figure(data=data,
layout=Layout(title="Calculated rates",
yaxis = {'title':'Production rate [mmol / h]'})
)
iplot(fig)
# plt.plot(t,single_trial.analyte_dict[analyte].gradient)
# plt.legend(keys)
Specific Productivity¶
The specific productivity is the rate, normalized to biomass concentration. This is the value used by dFBA to calculate the initial growth curves.
Here we find the median specific productivity and compare it to the FBA solutions
In [5]:
exchange_keys = biomass_keys + substrate_keys + product_keys
median_specific_productivity = {}
model_specific_productivity = {}
for analyte in exchange_keys:
model_specific_productivity[analyte] = model.solution.x_dict[analyte]
median_specific_productivity[analyte] = np.median(single_trial.analyte_dict[analyte].specific_productivity.data)
trace = Bar(x=[analyte for analyte in median_specific_productivity],
y=[median_specific_productivity[analyte] for analyte in median_specific_productivity],
name = 'Calculated')
trace2 = Bar(x=[analyte for analyte in model_specific_productivity],
y=[model_specific_productivity[analyte] for analyte in model_specific_productivity],
name = 'Model')
data = [trace, trace2]
fig = Figure(data=data,
layout=Layout(title="Calculated vs Model Specific Productivity",
yaxis = {'title':'Specific Productivity [mmol / (gdw h)]'})
)
iplot(fig)
Here we can see that the specific productivities match those calculated in the COBRA model (which is expected since that’s where the generated data came from). For cells in steady-state, this should be a constant.
Metabolic Model Integration¶
With specific productivities, metabolic model integration becomes straightforward. We can constrain the export fluxes based on the data, and solve the missing fluxes. Since this is model-generated data, this will close the mass balance entirely.
For experimental data, this offers a prediction to help close the balance.
In [6]:
# Let's take the model and add bounds for the known reactions
for analyte in analyte_keys:
with_noise = np.median(single_trial.analyte_dict[analyte].specific_productivity.data)
print(analyte,' ',with_noise)
model.reactions.get_by_id(analyte).lower_bound = with_noise
model.reactions.get_by_id(analyte).upper_bound = with_noise
print('\n\n\n')
solution = model.optimize()
model.summary()
Ec_biomass_iJO1366_core_53p95M 0.253954350914
EX_glc_e -10.5156403117
EX_for_e 18.1745176554
EX_ac_e 8.63085041752
EX_etoh_e 8.49418640731
EX_succ_e 0.0841767249714
IN FLUXES OUT FLUXES OBJECTIVES
glc__D_e -10.52 h_e 29.31 Ec_biomass_iJO1366_core_53p95M 0.254
nh4_e -2.74 for_e 18.17
h2o_e -1.80 ac_e 8.63
pi_e -0.24 etoh_e 8.49
co2_e -0.09 succ_e 0.08
so4_e -0.06 5drib_c 0.00
k_e -0.05 glyclt_e 0.00
mg2_e -0.00 mththf_c 0.00
fe2_e -0.00 4crsol_c 0.00
fe3_e -0.00 meoh_e 0.00
ca2_e -0.00 amob_c 0.00
cl_e -0.00
cu2_e -0.00
mn2_e -0.00
zn2_e -0.00
ni2_e -0.00
mobd_e -0.00
cobalt2_e -0.00
dFBA Batch Integration¶
We can integrate the experimental data across the course of the batch, and solve an FBA for each point to account for any misisng metabolites and get a dynamic flux map for the batch.
In [7]:
# dFBA based batch simulation
# import copy
# model2 = copy.deepcopy(model)
# impact.helpers.synthetic_data.dynamic_model_integration(t, y0, model2, single_trial, biomass_keys, substrate_keys, product_keys, extra_points_multiplier = 5)
Carbon Balance¶
From here, the carbon balance is straight forward. The export fluxes match experimental data, the remaining fluxes are estimated, and we can complete the carbon balance. Units are import here, and should all be converted a standard mass unit (g/L) to complete the balance.
In [8]:
# Convert mmol/gdw - hr to g / gdw - hr
# Create a dictionary for the mapping of flux reactions to metabolite names to get the molar mass
metabolite_export_reaction_dict = {
'EX_for_e':'for_e',
'EX_ac_e':'ac_e',
'EX_etoh_e':'etoh_e',
'EX_glc_e':'glc__D_e',
'EX_succ_e':'succ_e'
}
mass_flux = {}
for analyte in product_keys+substrate_keys:
mass_flux[analyte] = model.solution.x_dict[analyte] \
* model.metabolites.get_by_id(metabolite_export_reaction_dict[analyte]).formula_weight
mass_flux[biomass_keys[0]] = model.solution.x_dict[biomass_keys[0]]*1000
print(mass_flux)
# The balance is the sum of all metabolites, the uptake is already negative.
balance = sum(mass_flux[metabolite] for metabolite in mass_flux)
print(balance)
# The closure is the total substrate accounted for
percent_closure = balance/mass_flux['EX_glc_e']
print('\nThe mass balance is %f%% closed' % ((1-percent_closure)*100))
print(mass_flux)
# Two situations
# 1: balance is > 100% (must be some unaccounted substrate)
labels = [analyte.split('_')[1] for analyte in mass_flux]
print(percent_closure)
if percent_closure < 0:
fig = {
'data': [{'labels': labels + ['Unaccounted substrate'],
'values': [mass_flux[metabolite] for metabolite in mass_flux]+[balance],
'type': 'pie'}],
'layout': {'title': 'Mass balance'}
}
# 2: balance is < 100% (must be some unaccounted product)
else:
fig = {
'data': [{'labels': labels + ['Missing product'],
'values': [mass_flux[metabolite] for metabolite in mass_flux]+[abs(balance)],
'type': 'pie'}],
'layout': {'title': 'Mass balance'}
}
iplot(fig)
analyte_keys = substrate_keys + biomass_keys + product_keys
# Calculate the waterfall for the products and biomass
substrate_consuming_keys = biomass_keys+product_keys
running_total = balance
base = []
for i, key in enumerate(analyte_keys):
if i == 0:
running_total += -mass_flux[key]
base.append(0)
else:
base.append(running_total)
running_total += -mass_flux[key]
base_trace = Bar(x=analyte_keys,
y=base,
marker=dict(color='rgba(1,1,1, 0.0)',))
substrate_trace = Bar(x=[substrate_keys[0]],
y=[-mass_flux[substrate_keys[0]]],
marker=dict(color='rgba(55, 128, 191, 0.7)',
line=dict(color='rgba(55, 128, 191, 1.0)',
width=2,)))
biomass_trace = Bar(x=[biomass_keys[0]],
y=[-mass_flux[biomass_keys[0]]],
marker=dict(color='rgba(50, 171, 96, 0.7)',
line=dict(color='rgba(50, 171, 96, 1.0)',
width=2,)))
products_trace = Bar(x=product_keys,
y=[-mass_flux[metabolite] for metabolite in product_keys],
marker=dict(color='rgba(219, 64, 82, 0.7)',
line=dict(color='rgba(219, 64, 82, 1.0)',
width=2,)),
)
balance_base_trace = Bar(x=['Balance'],
y=[base[1]-balance],
marker=dict(color='rgba(1,1,1, 0.0)',))
balance_trace = Bar(x=['Balance'],
y=[balance],
marker=dict(color='rgba(0, 0, 0, 0.7)',
line=dict(color='rgba(0, 0, 0, 1.0)',
width=2,)),
)
data = [substrate_trace, balance_base_trace, base_trace, balance_trace, biomass_trace,products_trace]
layout = Layout(barmode='stack',
# paper_bgcolor='rgba(245, 246, 249, 1)',
# plot_bgcolor='rgba(245, 246, 249, 1)',
yaxis={'title': 'Exchange rate (mmol/(gdw h))'},
showlegend=False
)
fig = Figure(data=data,layout=layout)
iplot(fig)
{'EX_ac_e': 509.60010466932226, 'EX_for_e': 818.1702580800724, 'EX_etoh_e': 391.31391685379504, 'Ec_biomass_iJO1366_core_53p95M': 253.95435091418017, 'EX_glc_e': -1894.4544341121223, 'EX_succ_e': 9.770574289158397}
88.35477069440606
The mass balance is 104.663864% closed
{'EX_ac_e': 509.60010466932226, 'EX_for_e': 818.1702580800724, 'EX_etoh_e': 391.31391685379504, 'Ec_biomass_iJO1366_core_53p95M': 253.95435091418017, 'EX_glc_e': -1894.4544341121223, 'EX_succ_e': 9.770574289158397}
-0.04663863595949483
Flux mapping with escher¶
More detail is provided in the escher documentation: http://nbviewer.jupyter.org/github/zakandrewking/escher/blob/master/docs/notebooks/COBRApy%20and%20Escher.ipynb
In [9]:
import escher
import json
from IPython.display import HTML
In [10]:
b = escher.Builder(map_name='iJO1366.Central metabolism',
reaction_data=solution.x_dict,
# color and size according to the absolute value
reaction_styles=['color', 'size', 'abs', 'text'],
# change the default colors
reaction_scale=[{'type': 'min', 'color': '#cccccc', 'size': 4},
{'type': 'mean', 'color': '#0000dd', 'size': 20},
{'type': 'max', 'color': '#ff0000', 'size': 40}],
# only show the primary metabolites
hide_secondary_metabolites=True)
b.display_in_notebook()
Out[10]: